问题现状背景
数据管理应用需要整合多个来源的数据,这些多个来源的数据有可能冲突,为了提供数据的质量,需要解决冲突以及发掘反应真实世界的values,这个过程也叫做数据融合。
传统的方法是投票
论文的贡献(解决的问题)
本文提出了一种在大量有冲突的数据源中发现true values的数据融合方法,并且数据源之间可以copy。
- 考虑数据源之间copy的情况(但不支持两个数据源互相copy)
- truth discovery准确率提高
- 可扩展到大数据源的情况
举例
本文用一个例子,详细的对应计算贯穿全文,便于理解。
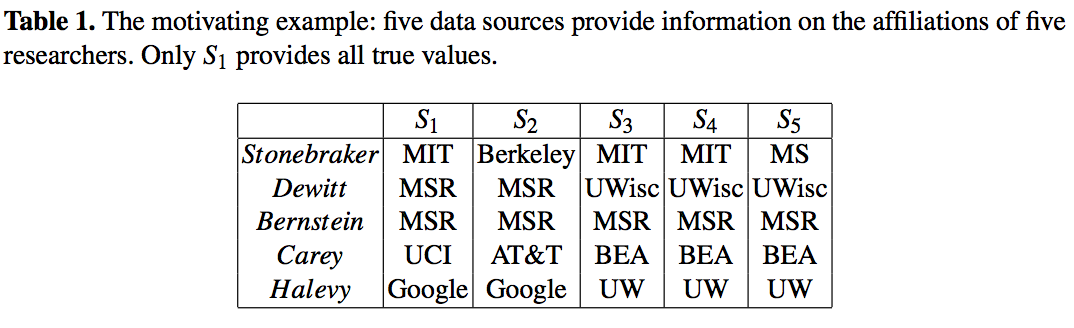
主要方法/特征
Intuition:
- 共享正确的值不一定表明copy,但如果两个源独立则共享错误值是一个低概率事件。
- 考虑投票的准确性(数据源的准确性用概率表示,需要鉴别数据源的独立性以及哪个源是copier)
Source Accuracy in data fusion
Problem: 给定数据源,对于每一个object确定其true value
计算一个数据源的准确性概率:
将数据源S的accuracy记作A(S),计算方式为源中所有值为真的平均概率,S提供一个特定错误值的概率为(1-A(S))/n。
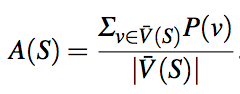
计算一个value为真的概率:
采用贝叶斯概率计算一个值为真的概率P(v)=Pr(v true/O的所有观察值),通过计算先验概率Pr(O的所有观察值/v true),Pr(O的所有观察值)
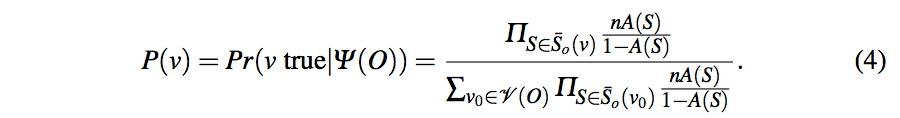
为了简化计算,v的置信度(confidence)记作C(v),数据源的准确分数记作A’(S),则C(v)为所有数据源分数的求和,P(v)也可以用C(v)表示。
Copying relationships in data fusion
分两种数据源:独立和有copy关系。
两个数据源提供的值分三种情况:Ot表示S1和S2提供相同的true value;Of表示S1和S2提供相同的false value;Od表示S1和S2提供different value;这三种value集合共同构成Phi空间。
依然采用贝叶斯概率,分别计算Pr(Phi/S1与S2独立),Pr(Phi/S1->S2),Pr(Phi/S2->S1),可由此计算Pr(S1与S2独立/Phi)
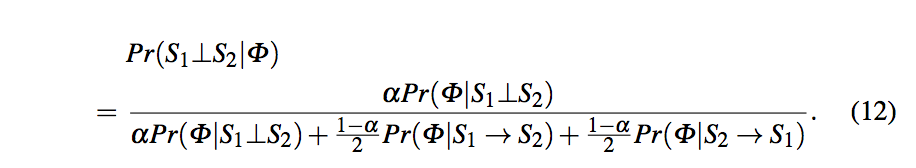
Independent Vote Count of a Value
即使copier也会提供不同于原始源的值,我们会计算每个值的independent vote。首先,采用一种贪心算法去决定所有源独立性的排序,越独立的排序越靠前。然后,再计算S独立的提供v相较于其他源S0提供v的概率,I(S)。则v的confidence为,C(v) = A’(S)*I(S)对所有源的求和。
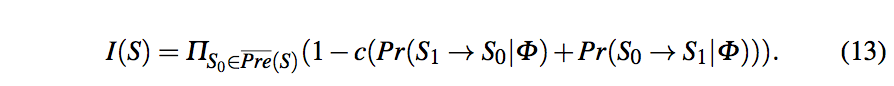
Iterative Algorithm - ACCUCOPY
迭代计算:accuracy of sources, copying between sources, and confidence of values
初始状态给每个源初始化相同的准确度,每个value相同的正确概率。1)根据前次的C(v)计算copying关系;2)更新C(v);3)更新源的准确度。
最多2l*n0轮收敛(l为object个数,n0为每个源的value个数),每轮的时间复杂度为O(object的个数x源的个数的平方xlog(源的个数))
效果结论
http://lunadong.com/fusionDataSets.htm上AbeBooks.com各个书店的计算机类图书书单。
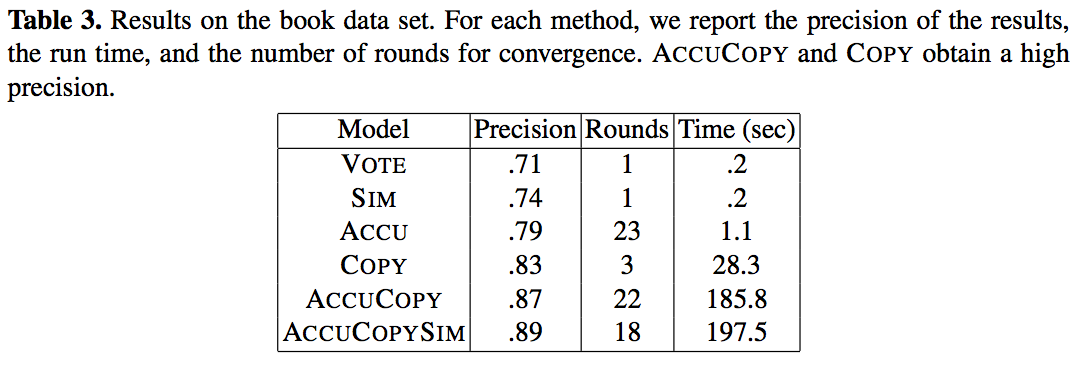
我的总结
原先的判断true value的投票算法并未考虑源之间互相抄袭的情况,本文的算法中考虑了这种情况后,准确率大大提高。